| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 티스토리챌린지
- BPDU
- freeradius
- stream 9
- Ansible
- 네이티브 vlan
- Red Hat
- 프로그래머스
- 방화벽
- Network Design
- SQL
- 네트워크 설계
- ospf
- LACP
- port aggregation protocol
- centos
- pvst+
- eigrp
- gns3
- vlan
- rommon mode
- junos os
- STP
- Cisco
- pagp
- ansible playbook
- 네트워크
- Packet Tracer
- 오블완
- 하프오픈
- Today
- Total
Doctor Pepper
네트워크의 기본 정의 (1) 본문
1. 기본 정의
네트워크 또는 그래프는 노드(Node)와 링크(Link)로 구성된다.
| 노 드 | 네트워크를 이루는 각 점을 나타냄 |
| 링 크 | 노드 간의 관계나 상호작용을 연결하는 선임 |
노드와 링크는 의사소통, 사회적 관계, 물리적 연결, 지리적 위치, 개념적 연관, 화학적 결합, 생물학적 상호작용 등을 표현할 수 있다. 두 노드가 링크로 연결되어 있다면 인접 또는 연결되어 있다고 하며, 이와 같은 노드들을 이웃(Neighbor)이라고 부른다.
| ※ 참고 : 네트워크의 정의 네트워크(Network)는 두 가지 기본 요소로 구성된다. 첫째, 노드(Node)는 네트워크의 구성 요소로, 일반적으로 꼭짓점(Vertex)이라고도 불리며, N개의 노드 집합으로 표현된다. 둘째, 링크(Link) 또는 에지(Edge)는 L개의 노드 쌍으로 구성되며, 한 노드에서 다른 노드로의 연결을 나타낸다. 네트워크는 방향성을 가질 수도 있고, 그렇지 않을 수도 있다. 방향성 네트워크(Directed Network)는 유향 그래프(Directed Graph)라고도 불리며, 링크는 방향성 링크(Directed Link)로 표현된다. 이 경우, 각 링크는 특정 원천 노드(Source Node)에서 목표 노드(Target Node)로의 이동을 나타낸다. 반면, 방향이 없는 네트워크(Undirected Network)에서는 링크가 양방향으로 작동하며, 링크에 포함된 두 노드의 순서는 중요하지 않다. 또한, 네트워크는 가중치(Weight)를 가질 수도 있다. 가중치 네트워크(Weighted Network)에서는 각 링크에 대해 가중치가 할당되며, 이를 통해 각 링크가 가지는 중요도나 비용을 표현할 수 있다. 이 경우, 가중치 링크(Weighted Link)는 노드 간의 연결에 추가적인 값을 부여한다. 네트워크는 방향성과 가중치를 모두 가질 수도 있으며, 이 경우 이를 방향성 가중치 링크(Directed Weighted Link)라고 부른다. |
- 네트워크의 특징
네트워크는 시스템 내의 다양한 관계를 효과적으로 설명하기 위한 개념적 도구로, 다음과 같은 학문적 배경과 연구 전통을 가진다.
- 수학, 컴퓨터 과학, 사회학, 커뮤니케이션에서 오래된 연구 역사가 있다.
- 물리학, 생물학에서는 최근 들어 네트워크를 통한 연구가 활발히 진행되고 있다.
- 분야별로 네트워크에 대한 명칭이 다를 수 있다(그래프(Graph): 네트워크, 꼭짓점(Vertex) : 노드, 에지(Edge) : 링크).
18세기 수학자 레온하르트 오일러(Leonhard Euler)의 그래프 이론에서 유래된 개념이다.
- 네트워크를 정의하는 요소
네트워크는 두 가지 주요 요소로 정의된다.
| 노드 수(N) | 네트워크를 구성하는 노드의 총 개수, 즉 네트워크의 크기(Size)를 의미함 |
| 링크 수(L) | 노드 간 연결을 나타내는 링크의 총 개수를 의미함 |
- 네트워크 유형
노드와 링크의 특성에 따라 다양한 네트워크가 정의된다.
| 방향성 네트워크 (Directed Network) |
- 링크에 방향이 있는 네트워크. - 예: 위키백과에서 문서 간 하이퍼링크. |
| 무향성 네트워크 (Undirected Network) |
- 링크에 방향이 없는 네트워크. - 예: 페이스북의 친구 관계. |
| 가중치 네트워크 (Weighted Network) |
- 링크에 가중치(Weight)가 부여된 네트워크. - 예: 이메일 트래픽에서 데이터 양을 나타내는 링크. |
| 방향성있는 가중치 네트워크 (Directed and Weighted Network) |
- 방향과 가중치를 모두 가진 네트워크. - 예: 이메일 네트워크(발신-수신 관계와 통신 트래픽). |
| 이분 네트워크 (Bipartite Network) |
- 서로 다른 두 종류의 노드로 구성된 네트워크. - 한 그룹의 노드와 다른 그룹의 노드만 연결 가능. - 예: 영화-배우, 노래-가수, 제품-고객 관계. |
| 다중 네트워크 (Multiplex Network) |
- 여러 종류의 링크를 가진 네트워크. - 예: 위키백과에서 하이퍼링크와 조회수, 수정 이력 간의 관계를 표현. |
- 활용 예
네트워크는 다양한 시스템의 구조와 관계를 분석하는 데 사용된다.
| 소셜 네트워크 | 사람 간 관계 분석 |
| 통신 네트워크 | 데이터 송수신 구조 |
| 생물학적 네트워크 | 유전자 및 단백질 상호작용 |
| 물리적 네트워크 | 항공, 도로 등 물리적 연결 구조 |
2. 프로그램 코드를 이용한 다양한 네트워크
네트워크를 효과적으로 관리하고 시각화하려면 소프트웨어 도구를 활용하거나 직접 프로그램 코드를 작성해야 한다. 현재 여러 프로그래밍 언어에 네트워크 처리를 지원하는 라이브러리와 네트워크 분석 및 시각화 도구들이 존재한다. 본 게시글은 파이썬의 네트워크 라이브러리 NetworkX를 사용하여 다양한 네트워크를 생성하고 다루는 방법을 소개한다.
| NetworkX 기능 | - 네트워크 데이터 구조 - 알고리즘 - 네트워크 측정 및 생성 함수 - 기초적인 시각화 기능 |
- 무방향 네트워크 생성
NetworkX를 사용하면 방향이 없는 무방향 네트워크를 간단히 생성하고 노드와 링크를 추가할 수 있다.
| impoer networkx as nx # 방향이 없는 그래프 생성 G = nx.Graph() # 노드와 링크 추가 G.add_node(1) # 노드 1 추가 G.add_node(2) # 노드 2 추가 G.add_edge(1,2) # 노드 1과 2를 연결하는 링크 추가 |
여러 개의 노드와 링크를 한 번에 추가할 수도 있다.
| # 여러 노드 추가 G.add_nodes_from([3, 4, 5]) # 여러 링크 추가 G.add_edges_from([(3, 4). (3, 5)] |
- 노드와 링크 확인
네트워크의 구성요소를 확인하고 이웃 노드의 리스트를 출력할 수 있다.
| G.nodes() # 네트워크의 모든 노드 G.edges() # 네트워크의 모든 링크 G.neighbors(3) # 노드 2의 이웃 노드 |
- 네트워크 순회
모든 노드와 링크를 순회하며 정보를 출력할 수 있다.
| # 노드 순회 for n in G.nodes: print(n, G.neighbors(n)) # 링크 순회 for u, v in G.edges: print(u, v) |
- 방향성 네트워크 생성
방향성 네트워크는 링크의 방향이 중요한 경우 사용된다.
| # 방향성 그래프 생성 D = nx.DiGraph() # 방향성 링크 추가 D.add_edge(1, 2) # 노드 1에서 2로의 링크 D.add_edge(2, 1) # 노드 2에서 1로의 링크 D.add_edges_from([(2, 3), (3, 4)]) |
방향성 네트워크에서는 링크의 방향에 따라 다른 동작을 할 수 있다. 또한, 링크를 추가할 때 해당 노드가 없으면 자동으로 노드가 생성된다.
| D.number_of_nodes() # 총 노드 수 D.number_of_edges() # 총 링크 수 |
노드와 연결된 이웃을 구할 때는 두 가지 함수로 구분할 수 있다.
- predecessors(node): 해당 노드로 들어오는 링크의 노드
- successors(node): 해당 노드에서 나가는 링크의 노드
| D.neighbors(2) # 노드 2와 연결된 이웃 D.predecessors(2) # 노드 2로 들어오늘 링크의 노드 D.successors(2) # 노드 2에서 나가는 링크의 노드 |
- 다양한 네트워크 생성
NetworkX는 여러 유형의 네트워크를 생성하는 기능을 제공한다. 각 네트워크 생성 시, 노드나 링크 수와 같은 기본적인 정보를 지정해주어야 한다.
| # 이분 네트워크 B = nx.complete_bipartite_graph(4, 5) # 두 그룹: 4개의 노드와 5개의 노드 # 순환 그래프 C = nx.cycle_graph(5) # 노드 5개로 이루어진 순환 그래프 # 경로 그래프 P = nx_path_graph(5) # 노드 5개로 이루어진 경로 그래프 # 스타 그래프 S = nx.star_graph(5) # 중심 노드와 5개의 연결된 노드로 구성 |
3. 네트워크의 조밀도와 성김도
네트워크의 구조를 이해하는 중요한 개념 중 하나는 조밀도(Density)와 성김도(Sparsity)이다.
- 최대 링크 수와 완전 네트워크
네트워크에서 최대 링크 수는 시스템의 노드 사이에 가능한 모든 연결의 개수로 제한된다.
- 최대 링크 수 : 노드 쌍의 수로 계산된다.
- 여기서, N은 네트워크의 노드 수
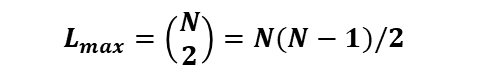
모든 가능한 노드 쌍이 서로 연결된 네트워크를 완전 네트워크(Complete Network)라고 한다. 완전 네트워크는 모든 가능한 링크를 포함하고 있어 가장 높은 조밀도를 가지며, 이 조밀도 값은 1이다.
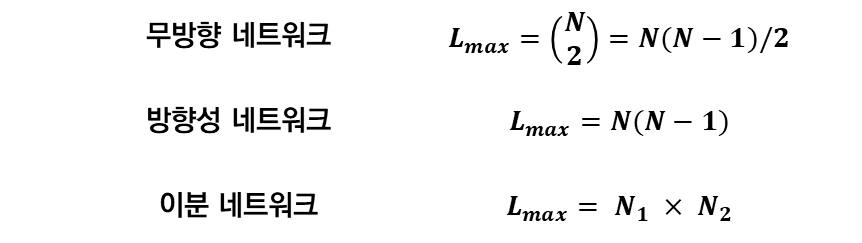
| 무방향 네트워크 | - 최대 링크 수는 구분 가능한 노드 쌍의 수로 계산됨 - 각 노드는 N−1개의 다른 노드와 연결될 수 있음 - 노드가 N개 있으므로 전체 링크 수는 N(N−1)임 - 하지만 이 방법은 각 연결을 두 번 세므로, 2로 나눠야 함 |
| 방향성 네트워크 | - 각 노드 쌍에 대해 방향이 다른 두 연결이 존재할 수 있음 - 따라서, 링크 수는 다음과 같이 계산됨. |
| 이분 네트워크 | - 두 그룹의 노드가 각각 다른 그룹의 모든 노드에 연결되면 완전 이분 네트워크임 |
- 조밀도와 성김도 정의
- 조밀도(Density) : 네트워크에서 실제로 존재하는 링크의 수를 최대 링크 수로 나눈 비율을 나타낸다.
- 여기서, L은 실제 링크수
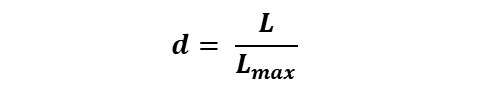
실제로 많은 네트워크는 완전 네트워크와 비교하여 조밀도가 매우 낮다. 대부분의 노드 쌍은 서로 직접 연결되지 않기 때문에, 링크의 실제 수는 최대 링크 수에 비해 훨씬 적다.

- 원전 네트워크의 경우, 링크 수 L=L_max이므로, 조밀도 d = 1이다.
- 성긴 네트워크의 경우, 실제 링크 수 L ≪ L_max이므로, 조밀도 d ≪ 1이다.
| 네트워크 크기와 링크 수 증가 관계 |
네트워크가 커질수록 (N 증가), 링크 수 L의 증가 속도로 조밀함 또는 성김을 구분할 수 있음 - 성긴 네트워크: L∼N 또는 L이 보다 더 느리게 증가함. - 조밀 네트워크: L∼N^2 또는 L이 N^2보다 빠르게 증가함. |
조밀도가 낮은 네트워크는 성김도(Sparsity)라는 특성을 가진다. 직관적으로, 네트워크에 링크가 적을수록 성김도가 높다.
- 소셜 네트워크의 성김도 예시
페이스북 네트워크에는 약 20억 (N ≈ 2 × 10^9)명의 사용자가 있다.
만약 페이스북의 완전 네트워크라면
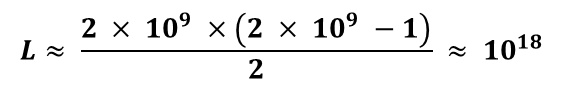
즉, 약 10^18개의 링크가 필요하다. 이는 저장하거나 처리하기 어려운 엄청난 데이터 크기이다.
그러나 실제로 소셜 네트워크는 매우 성기며, 페이스북에서도 각 사용자가 평균적으로 약 1000명 이하의 친구를 가지진다. 따라서 페이스북 네트워크의 조밀도는
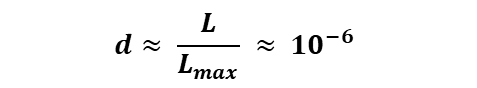
이렇게 조밀도가 낮은 덕분에 페이스북은 데이터 관리를 효율적으로 수행할 수 있다.
- NetworkX를 이용한 조밀도 계산
NetworkX는 방향성 네트워크와 방향성이 없는 네트워크의 조밀도를 계산하는 기능을 제공한다. 이를 활용하여 네트워크의 조밀도를 간단히 확인할 수 있다.
| import network as nx # 무방향 네트워크 조밀도 계산 G = nx.Graph() G.add_edges_from([(1, 2), (2, 3), (3, 4), (4,1)]] print(nx.density(G)) # 방향성 네트워크 조밀도 계산 D = nx.DiGraph() D.add_edges_from([(1, 2), (2, 3), (3, 1)]) print(nx.density(D)) # 완전 네트워크 조밀도 계산 CG = nx.complete_graph(8471) print(nx.density(CG)) |
4. 서브 네트워크(Subnetwork)
네트워크의 연구에서 종종 전체 네트워크가 아닌 특정 부분집합에 관심을 가지게 된다. 이 부분집합 자체가 하나의 네트워크로, 서브네트워크(Subnetwork) 혹은 부분 그래프(Subgraph)라 부른다. 서브네트워크는 네트워크의 노드 부분집합과 이 노드들 사이의 모든 링크로 구성된다. 다양한 유형의 서브네트워크는 실제 네트워크의 구조와 성질을 이해하는 데 중요한 역할을 한다.
- 서브네트워크의 유형
| 클리크(Clique) | 클리크는 노드 부분집합 내에서 모든 노드가 서로 연결된 완전 서브네트워크임. 완전 네트워크에서는 모든 노드가 연결되어 있으므로, 그 서브네트워크 또한 모두 클리크가 됨. 클리크의 크기와 분포는 네트워크 구조 분석에 중요한 지표로 활용됨. |
| 자기주변 네트워크 (Ego Network) |
특정 노드(에고, Ego)를 중심으로, 해당 노드와 직접 연결된 이웃 노드들로 구성된 서브네트워크임 자기주변 네트워크는 특히 소셜 네트워크 분석에서 빈번하게 연구되며, 개인의 연결성과 관계의 밀도를 평가하는 데 유용함 |
- NetworkX를 이용한 서브네트워크 생성
NetworkX는 주어진 네트워크에서 노드의 부분집합을 지정하여 서브네트워크를 생성할 수 있는 기능을 제공한다.
| import networkx as nx # 완전 그래프 생성 K5 = nx.complete_graph(5) # 특정 노드들로 서브 네트워크 생성 clique = nx.subgraph(K5, [0, 1, 2]) # 서브네트워크의 노드와 연결 정보 출력 print(list(clique.nodes)) print(list(clique.edges)) |
5. 연결선 수
연결선 수(Degree)는 네트워크 내 특정 노드가 가지는 링크 혹은 이웃의 개수를 나타내며, 노드 의 연결선 수는 k_i로 표기된다.
- 연결선 수의 특징
| 노드별 연결선 수 | 노드의 연결선 수는 네트워크에서 해당 노드의 중요도와 관계를 이해하는 데 사용됨. 연결선 수가 0인 노드는 싱글톤(Singleton)이라 불리며, 다른 노드와 연결되지 않은 독립된 노드임. |
| 평균 연결선 수 | 네트워크의 평균 연결선 수는 ⟨k⟩\langle k \rangle로 표기되며, 이는 네트워크의 조밀도와 직접적으로 관련됨. |
- 평균 연결선 수 공식
- 여기서, L은 네트워크의 총 링크 수, N은 노드 수
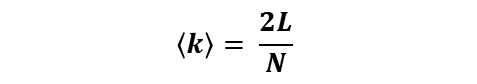
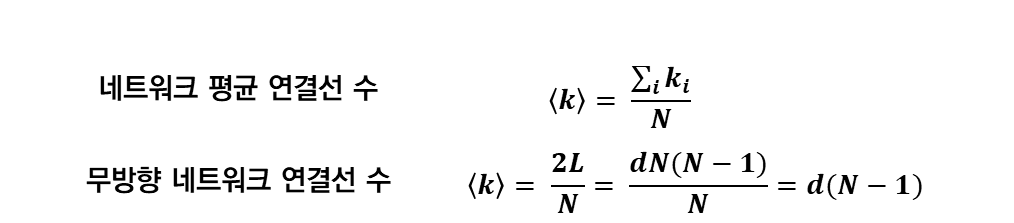
| 무방향 네트워크 연결선 수 | 무방향 네트워크의 조밀도 식에 의해 2L = dN(N-1)이됨 그러나, 무방향 네트워크 연결선 수의 역인 d=<k>/(N-1)은 될 수 없음 - 조밀도는 평균과 최대 연결 수의 비율임 |
- NetworkX를 사용한 연결선 수 계산
NetworkX는 특정 노드의 연결선 수를 계산하거나 네트워크 내 모든 노드의 연결선 수를 반환하는 기능을 제공한다
| # 무방향 그래프 생성 G = nx.Graph() G.add_edges_from([(1, 2), (2, 3), (3, 4), (4, 1), (1, 3)]) # 특정 노드의 연결선 수 print(G.degree(2)) # 모든 노드의 연결선 수 degree_dict = dict(G.degree()) print(degree_dict) |
'Network 심화 > 네트워크 분석' 카테고리의 다른 글
| 중심도(Centrality) (0) | 2024.11.29 |
|---|---|
| 네트워크 특징 (2) : 트리 및 최단 경로 찾기 (3) | 2024.11.27 |
| 네트워크 특징 (1) : 동류성 및 경로와 거리 (2) | 2024.11.26 |
| 네트워크의 기본 정의 (2) (1) | 2024.11.25 |




