| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 오블완
- stream 9
- 네이티브 vlan
- 방화벽
- Ansible
- vlan
- junos os
- rommon mode
- eigrp
- ansible playbook
- Cisco
- ospf
- pagp
- port aggregation protocol
- Red Hat
- 하프오픈
- freeradius
- 프로그래머스
- STP
- Network Design
- 네트워크 설계
- 네트워크
- centos
- Packet Tracer
- 티스토리챌린지
- pvst+
- LACP
- SQL
- gns3
- BPDU
- Today
- Total
Doctor Pepper
중심도(Centrality) 본문
1. 중심성(중심도)
- 연결선 수 중심성(Degree Centrality) : 노드와 직접 연결된 이웃 노드 수
| 특징 | - 연결선 수가 많을수록 인맥이 넓고 중요성이 높음 - 평균 연결선 수는 노드 간 연결 정도를 나타내지만, 실제 분포의 불균일성을 제대라 반영하지 못할 수 있음 |
- 근접 중심성(Closeness Centrality) : 한 노드에서 다른 모든 노드까지의 거리 합의 역수
| 특징 | - 거리 합이 작을수록 네트워크 중심에 가까움 - 네트워크 내에서 빠르고 효율적인 정보 전달 가능성을 나타냄 |
- 노드의 근접 중심도
- 여기서, ℓ_ij는 i에서 j까지의 거리이고, 노드 i 자신을 제외한 네트워크의 모든 노드에 대한 합이다.

- NetworkX에서 근접 중심도
| nx.closeness_centrality(G, node) |
- 사이 중심도(Betweenness Centrality) : 최단 경로가 특정 노드를 통과하는 빈도를 기반으로 계산
| 특징 | - 중요한 통신 경로 역할을 하는 노드가 높은 사이 중심도를 가짐 - 네트워크 여러 지역을연결하는 노드는 적은 연결선 수에도 높은 사이 중심도를 가질 수 있음 |
| 링크 사이 중심성 | - 링크를 통과하는 최단 경로의 비율로 측정 - 커뮤니티를 연결하거나 구분하는 데 사용 |
- 노드 사이 중심도
- 여기서, σ_hj는 h 노드에서 j로 가는 최단 경로의 개수이다.

- NetworkX에서 노드와 링크의 정규화된 사이 중심도
| nx.betweenness_centrality(G) nx.edge_betweenness_centrality(G) |
- 중심성의 의의
- 중심성 측도는 네트워크 분석에서 각 노드와 링크의 상대적 중요성을 평가하는 데 핵심이다.
- 실제 네트워크에서 다양성과 복잡성을 반영하여 적합한 측도를 선택해야 한다.
2. 중심도 분포 : 네트워크 분석의 이해
- 소셜 네트워크의 초기 연구
온라인 소셜 미디어 등장 이전, 소셜 네트워크 연구는 개인 인터뷰와 설문조사를 통해 이루어졌다. 이로 인해 시간과 참여자의 제약으로 소규모 네트워크(수십 개의 노드)만을 다룰 수 있었다. 당시에는 "이 네트워크에서 가장 중요한 노드는 무엇인가?"와 같은 질문을 통해 네트워크 구조를 분석했다.
- 대규모 네트워크와 중심도 분포
오늘날 소셜 네트워크는 훨씬 더 커졌다. 예를 들어, 페이스북은 약 20억 명의 사용자를 포함하며, 이 중 유명 인사도 다수 포함되어 있다. 하지만 이러한 대규모 네트워크에서는 개별 노드의 중요성을 평가하기보다 중심도 분포를 통해 노드 간의 특성과 네트워크 구조를 이해하는 것이 중요하다.
통계적 분석은 개별 요소가 아닌 비슷한 속성을 공유하는 노드 및 링크 그룹에 주목한다. 이를 통해 연결선 수와 같은 중심도 값을 가진 노드들의 분포를 조사하고, 네트워크 구조에서 중요한 특징을 도출할 수 있다.
- 연결선 수 분포
네트워크에서 노드의 연결선 수는 네트워크 구조를 설명하는 핵심 요소이다. 연결선 수 분포는 특정 연결선 수를 가진 노드의 개수를 나타내며, 대규모 네트워크의 불균일도를 파악할 수 있다.
| 트위터 네트워크 | - 노드: 사용자 - 링크: 리트윗 관계 - 18,470개의 노드와 48,365개의 링크 (평균 연결선 수: 2.6) |
| 위키백과 네트워크 | - 노드: 페이지 - 링크: 하이퍼링크 - 15,220개의 노드와 194,103개의 링크 (평균 연결선 수: 12.8) |
이 두 네트워크는 성긴(sparse) 구조를 가지며, 이는 많은 실제 네트워크에서 관찰되는 특징이다.
- 두꺼운 꼬리 분포와 허브
대규모 네트워크에서는 연결선 수 분포가 광범위하며, 두꺼운 꼬리 분포를 나타내는 경우가 많다. 이는 대부분의 노드가 소수의 이웃만 가지지만, 허브(hub)라고 불리는 일부 노드가 많은 이웃을 가지는 구조를 말한다.
- 허브는 네트워크에서 중요한 역할을 하며, 자연계, 소셜 네트워크, 정보 네트워크에서 공통적으로 나타낸다.
- 불균일도와 방향성 네트워크
연결선 수의 불균일도를 측정하는 불균일도 매개변수는 네트워크 구조를 분석하는 데 중요한 지표이다.
| 불균일도가 높음 | 허브가 많고 네트워크의 연결선 수 다양성이 큼 |
| 불균일도가 낮음 | 연결선 수가 균일하게 분포됨 |
- 불균일도 : 연결선 수 제곱의 평균인 평균 제곱 연결선 수(Average squared degree)를 도입해야 한다.
- k_0라는 특정 값에서 뾰족한 봉우리가 있는 정규 분포(normal distibution) 또는 좁은 분포의 경우 연결선 수를 제곱한 값의 분포는 k_0^2 근처에 몰려 있을 것이다.
- 따라서,⟨k^2⟩ ≈ k_0^2이 되고 ⟨k⟩ ≈ k_0, κ ≈ 1이 된다 .
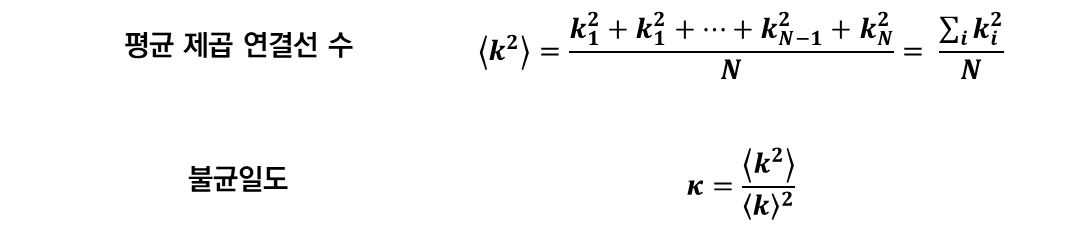
방향성이 있는 네트워크(트위터, 위키백과 등)에서는 들어오는 연결선 수(In-Degree)와 나가는 연결선 수(Out-Degree)를 모두 분석해야 한다.
- ex) 웹 페이지는 여러 페이지로부터 연결될 수 있지만(In-Degree 높음), 적은 수의 페이지로 링크를 보낼 수 있음(Out-Degree 낮음).
- 중심도 분석의 확장
연결선 수 외에도 다른 중심도 특성(예: 매개 중심성, 고유벡터 중심성 등)의 분포를 분석함으로써 네트워크 동역학 과정과 구조적 특징을 더 깊이 이해할 수 있다.
'Network 심화 > 네트워크 분석' 카테고리의 다른 글
| 네트워크 특징 (2) : 트리 및 최단 경로 찾기 (3) | 2024.11.27 |
|---|---|
| 네트워크 특징 (1) : 동류성 및 경로와 거리 (2) | 2024.11.26 |
| 네트워크의 기본 정의 (2) (1) | 2024.11.25 |
| 네트워크의 기본 정의 (1) (3) | 2024.11.25 |





