Notice
Recent Posts
Recent Comments
Link
250x250
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
Tags
- STP
- eigrp
- ansible playbook
- Network Design
- 네이티브 vlan
- ospf
- gns3
- 방화벽
- port aggregation protocol
- BPDU
- Ansible
- 티스토리챌린지
- 비대칭 경로
- pagp
- 헬스 체크
- vlan
- Cisco
- 프로그래머스
- SQL
- 패킷 필터링
- 네트워크
- 하프오픈
- LACP
- pvst+
- 오블완
- Packet Tracer
- campus network
- junos os
- 네트워크 설계
- 연결선 수
Archives
- Today
- Total
Doctor Pepper
네트워크 특징 (2) : 트리 및 최단 경로 찾기 본문
728x90
1. 트리
트리는 모든 링크를 제거하지 않고 단 하나의 링크만 삭제해도 네트워크가 두 개의 부분으로 나뉘는 특별한 형태의 무방향 연결 네트워크를 의미한다. 이러한 네트워크 구조를 트리(Tree)라고 부른다.
| 링크 수 | 트리의 노드가 n개라면, 항상 n-1개의 링크를 가짐 |
| 사이클 없음 | 트리에는 사이클(순환 경로)이 존재하지 않으며, 이를 귀류법으로 증명할 수 있음 - 만약 트리에 사이클이 존재한다고 가정하면, 사이클 내의 링크 중 하나를 제거하더라도 여전히 모든 노드가 연결된 상태를 유지할 수 있음 - 이 경우, 트리는 더 이상 링크를 하나 삭제해도 분리되지 않는 상태가 되며, 트리의 정의에 어긋남.(따라서, 트리는 사이클을 가질 수 없음) 사이클이 없기 때문에 트리의 임의의 두 노드를 연결하는 경로는 항상 하나만 존재함 |
| 계층적 구조 | - 트리의 임의의 노드를 선택하여 루트(Root)라고 정의할 수 있음 - 각 노드는 루트 방향으로 연결된 하나의 부모 노드와 루트에서 멀어지는 방향으로 연결된 하나 이상의 자식 노드를 가짐 - 단, 루트는 부모가 없으며, 리프(Leaf)는 자식이 없음 |

- NetworkX를 이용하여 트리 여부 확인
| import networkx as nx # 완전 그래프 K4 = nx.complete_graph(4) print(nx.is_tree(K4)) # False (사이클이 있음) # 사이클 그래프 C = nx.cycle_graph(4) print(nx.is_tree(C)) # False (사이클이 있음) # 경로 그래프 P = nx.path_graph(5) print(nx.is_tree(P)) # True (트리) # 별 그래프 S = nx.star_graph(6) print(nx.is_tree(S)) # True (트리) |
2. 최단 경로 찾기
두 노드 간의 최단 경로를 찾기 위해서는 네트워크 전체의 구조를 파악하고, 이를 바탕으로 길을 탐색하는 과정을 거친다. 이러한 작업은 NetworkX와 같은 네트워크 분석 도구를 활용하거나, 웹 크롤러(Web Crawler)처럼 네트워크 데이터를 수집하는 방식을 통해 수행할 수 있다.
- 너비 우선 탐색(Breadth-First Search, BFS)
너비 우선 탐색(BFS)은 원천 노드(Source Node)에서 출발해 네트워크 내 다른 모든 노드와의 최단 경로를 찾는 기본적인 알고리즘이다.
| 원천 노드 탐색 | 원천 노드에서 출발하여 이웃 노드를 방문함 이 노드들은 계층 1에 속하며, 원천 노드와의 거리는 1로 설정됨 |
| 계층별 탐색 | 계층 1의 이웃 노드를 방문하고, 이미 방문한 노드를 제외한 나머지 노드를 계층 2로 설정함. 이 노드들과 원천 노드 사이의 거리는 2가 됨 이 과정을 반복하여 각 계층의 노드를 탐색함 |
| 특징 | 각 계층에 속한 노드는 원천 노드와 동일한 거리를 가지며, 모든 노드가 방문될 때까지 탐색이 진행됨 연결된 네트워크라면 모든 노드가 탐색되며, 각 노드와 원천 노드 간의 최단 거리가 계산됨 |
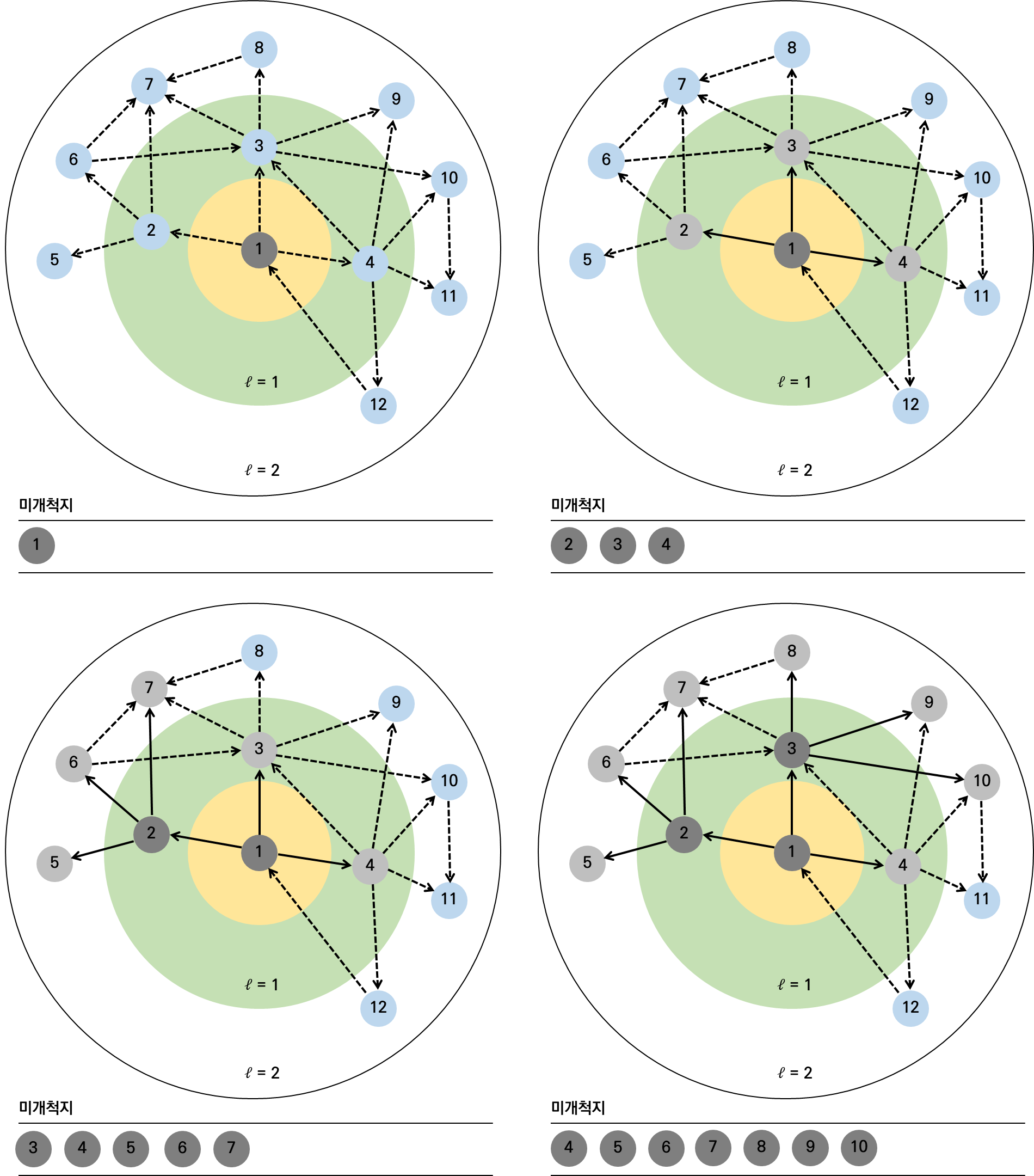
- 최단 경로 트리(Shortest-Path Tree)
BFS 알고리즘은 원천 노드를 루트로 하는 최단 경로 트리(Shortest-Path Tree)를 생성한다.
- 이 트리는 원천 노드와 다른 모든 노드 간의 최단 경로를 포함하는 링크들의 부분집합으로 구성된다.
- 트리의 각 노드는 고유한 이전 노드(Parent Node)를 가지며, 루트에서 시작하여 트리 상의 경로를 따라가는 방식으로 특정 노드까지의 최단 경로를 찾을 수 있다.
- 최단 경로 찾는 방법
| 원천 노드에서 목표 노드까지의 경로 찾기 | - 목표 노드에서 시작하여 트리 상의 이전 노드를 따라가면서 원천 노드에 도달함 - 이렇게 역방향으로 추적한 경로를 뒤집으면 최단 경로가 됨 |
| 무방향 네트워크 vs 방향성 네트워크 | - 무방향 네트워크에서는 목표 노드에서 원천 노드로의 최단 경로와 원천 노드에서 목표 노드로의 최단 경로가 동일함. - 반면, 방향성 네트워크에서는 경로가 다를 수 있음. |
- 가중치 네트워크에서의 최단 경로
BFS는 가중치가 없는 네트워크에서만 유효하다.
- 가중치 네트워크에서는 링크에 가중치가 부여되며, 이를 고려한 최단 경로 탐색이 필요하다.
- 이를 위해 다익스트라 알고리즘(Dijkstra's Algorithm)이나 벨만-포드 알고리즘(Bellman-Ford Algorithm)과 같은 방법을 사용한다.
- 모든 노드 쌍 간의 최단 경로
모든 노드 쌍 사이의 최단 경로를 찾으려면, 각 노드를 원천 노드로 설정해 BFS를 번 실행해야 한다. N은 네트워크의 노드 개수를 의미한다.
- 이 작업은 많은 계산이 필요하므로, 네트워크 크기가 클수록 효율적인 알고리즘 사용이 중요하다.
- 네트워크의 평균 경로 거리와 뭉침 계수 예
| 네트워크 | 노드 수(N) | 링크 수(L) | 평균 경로 길이(⟨ℓ⟩) | 뭉침 계수(C) |
| 노스웨스턴대학교 페이스북 | 10,567 | 488,337 | 2.7 | 0.24 |
| IMDB 영화와 주연배우 | 563,443 | 921,160 | 12.1 | 0 |
| IMDB 공동 출연 | 252,999 | 1,015,187 | 6.8 | 0.67 |
| 미국 정치 이슈 트위터 | 18,470 | 48,365 | 5.6 | 0.03 |
| 엔론 이메일 | 87,273 | 321,918 | 3.6 | 0.12 |
| 위키백과 수학 분야 | 15,220 | 194,103 | 3.9 | 0.31 |
| 인터넷 라우터 | 190,914 | 607,610 | 7.0 | 0.16 |
| 미국 항공 운송망 | 546 | 2,781 | 3.2 | 0.49 |
| 세계 항공 운송망 | 3,179 | 18,617 | 4.0 | 0.49 |
| 효모 단백질 상호작용 | 1,870 | 2,277 | 6.8 | 0.07 |
| 예쁜꼬마선충 신경망 | 297 | 2,345 | 4.0 | 0.29 |
| 에버글레이즈 생태 먹기 그물 | 69 | 916 | 2.2 | 0.55 |
728x90
'Network 심화 > 네트워크 분석' 카테고리의 다른 글
| 중심도(Centrality) (0) | 2024.11.29 |
|---|---|
| 네트워크 특징 (1) : 동류성 및 경로와 거리 (2) | 2024.11.26 |
| 네트워크의 기본 정의 (2) (1) | 2024.11.25 |
| 네트워크의 기본 정의 (1) (3) | 2024.11.25 |





